虚数i及其运算公式的探索（从高中数学到应用领域的重要性与应用前景）

虚数i是高中数学中一个重要的概念，它在解决无解实数方程、描述物理问题等方面有着广泛的应用。本文将围绕虚数i及其运算公式展开讨论，探究其在数学与应用领域中的重要性和潜力。

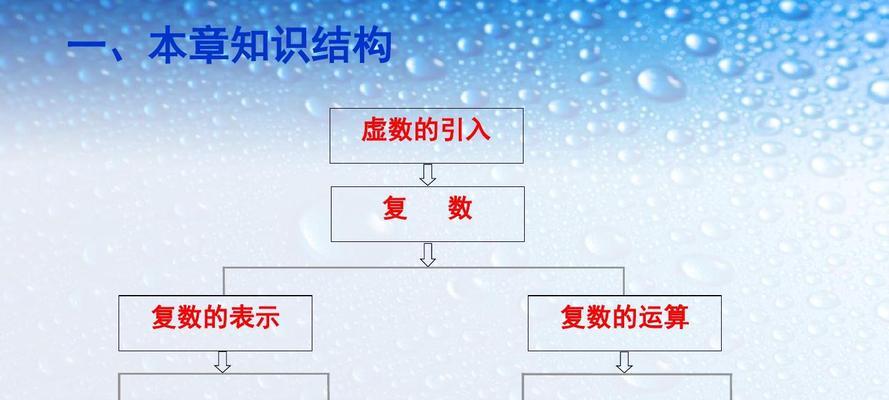
虚数i的引入及定义

虚数i是在解决无解实数方程时引入的，它定义为满足$i^2=-1$的数。通过引入虚数i，我们能够拓展实数域，进一步解决一些实数方程在实数范围内无解的问题。

复数的表示形式

虚数i与实数结合构成了复数，其一般表示形式为$a+bi$，其中$a$为实部，$b$为虚部。复数的表示形式使得我们能够对复数进行运算，进一步拓展了数学领域。

虚数单位i的性质

虚数单位i有着独特的性质，其中最重要的一点是$i^n$的周期性。当$n$为正整数时，$i^n$的值会循环出现，并最终回到初始状态。

虚数的加减法

虚数的加减法遵循了实数加减法的基本规则，即实部和虚部分别相加或相减。通过虚数的加减法，我们能够方便地进行复数的运算，解决一些实际问题。

虚数的乘法

虚数的乘法是通过将$i^2$替换为$-1$进行计算的。虚数乘法的运算结果是一个实数加上一个虚数，这个结果在物理学中有着重要的应用。

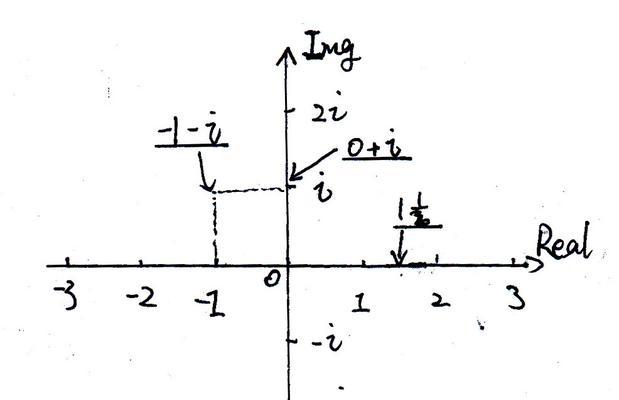
复数的共轭

复数的共轭是将其虚部取负得到的，即对于复数$a+bi$，它的共轭是$a-bi$。复数的共轭在运算中有着重要的作用，特别是在求复数的模、除法等方面。

复数的除法

复数的除法可以通过将分子和分母同时乘以分母的共轭来实现。复数的除法运算也在物理学中有广泛应用，例如在交流电路中的计算中常常涉及复数的除法。

复数在几何中的应用

复数可以用来表示平面上的点，实部表示横坐标，虚部表示纵坐标。通过复数在几何中的表示，我们能够方便地进行平面上的几何运算。

复数在物理中的应用

虚数i在物理学中有着广泛的应用，例如在量子力学中描述粒子的波函数、在电路分析中描述交流电路的阻抗等。虚数i的引入使得我们能够更好地描述和解决一些物理问题。

复数在信号处理中的应用

信号处理是现代通信技术中一个重要的领域，而复数在信号处理中有着广泛的应用。通过将信号表示为复数形式，我们能够方便地进行信号处理和调制解调等操作。

复数在控制系统中的应用

控制系统是自动控制领域中的一个重要组成部分，而复数在控制系统中有着重要的应用。通过将控制系统的响应表示为复数形式，我们能够方便地进行系统性能分析和设计。

虚数i的未来发展与挑战

虚数i作为一个重要的数学概念，在不同领域有着广泛的应用，但也面临着一些挑战。随着科学技术的不断发展，虚数i在更多领域的应用前景将不断扩大。

虚数i的教育意义与教学建议

虚数i的引入和运算公式是高中数学中重要的内容，它能够帮助学生拓宽数学思维和解决问题的能力。在教学中，我们应该注重理论与实际应用的结合，提高学生对虚数i的理解和应用能力。

虚数i的应用前景与社会影响

虚数i在科学、工程、通信等领域有着广泛的应用，它为现代社会的发展和进步做出了重要贡献。虚数i的进一步发展和应用将推动科技创新，对社会产生积极的影响。

虚数i及其运算公式是高中数学中的重要内容，它在数学领域和应用领域都有着广泛的应用。通过对虚数i的探索和理解，我们能够更好地解决实际问题，推动科学技术的发展。

转载请注明来自数科视界，本文标题：《虚数i及其运算公式的探索（从高中数学到应用领域的重要性与应用前景）》

标签：虚数